Musik ist die Kunst der ZEITMODULATION: Alles was wir an Tönen und Geräuschen wahrnehmen, hat stets auch eine zeitliche Dimension: d.h., es verändern sich innerhalb einer - meist sehr kurzen - Zeit Klangfarbe und Lautstärke.
Die (Amplituden)Hüllkurve ist das dynamische Profil eines Tones (Klanges, Geräusches)
z.B. Orchester Holz
Generell gesprochen, leitet sich aus dem Wort „Hüllkurve“ (engl.: Envelope) buchstäblich die Funktion dieses Bausteines zur Bearbeitung elektroakustischer Klänge ab: Etwas, das etwas Anderes einhüllt, umschließt und dabei verändert.
Die Mittel zur Modellierung dieses Umstandes stehen uns mit diversen Hüllkurven zur Verfügung.
Das sind nur einige Beispiele von heute erhältlichen Produkten. Ihre unterschiedliche Vielfalt zeigt, wie essentiell ihre Verwendung ist und wie phantasiereich sie sich entfalten kann.
Das folgende Sprachbeispiel stellt uns aber vor eine viel komplexere Aufgabe, als nur über Ein- und Ausschwingen bestimmen zu können:
Alles was wir hoeren by Bruno Liberda
Der Computer eröffnet uns neue Möglichkeiten und erlaubt uns mittels sogenannter graphischer Hüllkurven hochkomplizierte Kurvenformen im wahrsten Sinne des Wortes nachzuzeichnen:
wobei verschiedene Programme unterschiedliche Steuer- und Designmöglichkeiten bieten.
Im folgenden möchte ich an einem sehr abstrakten, dafür umso einleuchtenderen Beispiel demonstrieren, wie mächtig Hüllkurven sind. Unser rohes Ausgangsmaterial ist einfaches weisses Rauschen:
Rauschen- by Bruno Liberda
mit eine relativ simplen Hüllkurve, die sich wiederholt, verändern wir den gleichströmenden Lautstärkeverlauf
das klingt dann so:
Rauschen*Env by Bruno Liberda
der nächste Schritt: Wir multiplizieren diese Hüllkurve mit einer ganz einfachen, viel langsameren Hüllkurve
… was folgendes Bild ergibt
… und so klingt
Rauschen*Env*Env by Bruno Liberda
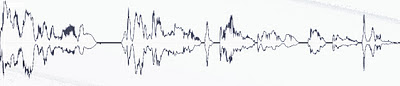
ein vorläufig letzter Schritt: mit der zweiten Hüllkurve steuern wir nicht nur die Amplitude der ersten, sondern lassen sie nun auch auf deren Ablaufgeschwindigkeit wirken – diese wird umso schneller, je kleiner die zweite Kurve wird
… und erhalten fast schon so etwas wie ein musikalisches Signal aus einfachen weissem Rauschen
Rauschen*Env*Env* by Bruno Liberda
nochmals der Weg vom rohen Klang hin zu einer rhythmisierten Figur schematisch zusammengefasst
z.B. Orchester Holz
Generell gesprochen, leitet sich aus dem Wort „Hüllkurve“ (engl.: Envelope) buchstäblich die Funktion dieses Bausteines zur Bearbeitung elektroakustischer Klänge ab: Etwas, das etwas Anderes einhüllt, umschließt und dabei verändert.
Die Mittel zur Modellierung dieses Umstandes stehen uns mit diversen Hüllkurven zur Verfügung.
Das folgende Sprachbeispiel stellt uns aber vor eine viel komplexere Aufgabe, als nur über Ein- und Ausschwingen bestimmen zu können:
Alles was wir hoeren by Bruno Liberda
Der Computer eröffnet uns neue Möglichkeiten und erlaubt uns mittels sogenannter graphischer Hüllkurven hochkomplizierte Kurvenformen im wahrsten Sinne des Wortes nachzuzeichnen:
wobei verschiedene Programme unterschiedliche Steuer- und Designmöglichkeiten bieten.
Im folgenden möchte ich an einem sehr abstrakten, dafür umso einleuchtenderen Beispiel demonstrieren, wie mächtig Hüllkurven sind. Unser rohes Ausgangsmaterial ist einfaches weisses Rauschen:
Rauschen- by Bruno Liberda
mit eine relativ simplen Hüllkurve, die sich wiederholt, verändern wir den gleichströmenden Lautstärkeverlauf
das klingt dann so:
Rauschen*Env by Bruno Liberda
der nächste Schritt: Wir multiplizieren diese Hüllkurve mit einer ganz einfachen, viel langsameren Hüllkurve
… was folgendes Bild ergibt
… und so klingt
Rauschen*Env*Env by Bruno Liberda
ein vorläufig letzter Schritt: mit der zweiten Hüllkurve steuern wir nicht nur die Amplitude der ersten, sondern lassen sie nun auch auf deren Ablaufgeschwindigkeit wirken – diese wird umso schneller, je kleiner die zweite Kurve wird
… und erhalten fast schon so etwas wie ein musikalisches Signal aus einfachen weissem Rauschen
Rauschen*Env*Env* by Bruno Liberda
nochmals der Weg vom rohen Klang hin zu einer rhythmisierten Figur schematisch zusammengefasst










Keine Kommentare:
Kommentar veröffentlichen